Deborah R. Fowler
"Trig Deeper" including dot product and
Pythagorean theorem
Posted on June 11 2022
Updated on June 15 2022
This is a continuation of the discussion of trigonometry but now with an object with thickness that doesn't pivot on the bottom line. Please click here the previous discussion.
Overview
This time I'm starting with my example file for intersection analysis. To start, let's simply but a box on top (base of the box is on the ground plane by using ch("sizey") * .5 in the center y parameter.
Exercise:
|

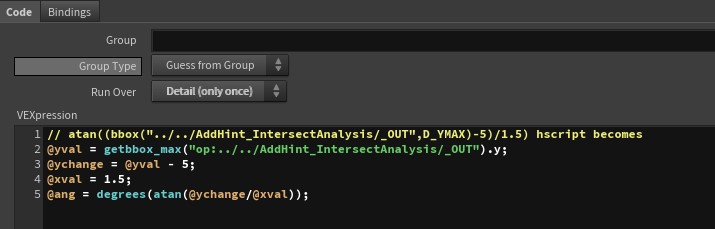
If we have a box that we want to rotate, if it is from the bottom, it is the same as we did before with atan( bbox D_YMAX of the tube - position in y of the box and then divided by the position in x)

So just like the butterfly example. This can be achieved with hscript or a point wrangle node.

| Exercise:
take your previous file and use both hscript and also
point wrangle to move the box. |
Now what if we didn't want the pivot point at the bottom? What if the box was to pivot based on the thickness.

In order to do this, we need to use the dot product. Quick review:
A vector has magnitude (length) and direction. The dot product between two vectors represents a scalar value that is the cosine of the angle between the vectors.
By definition, the dot product between
- vector a dot vector b = | vector a |
* | vector b | * cos angle
- where | vector | is the magnitude of the
vector
In wrangle nodes we have a function called dot
that allows us to enter the normalized vectors and returns the
dot product.
If we take the acos of that value and convert it to degrees
(since vex works in radians) we have our answer.
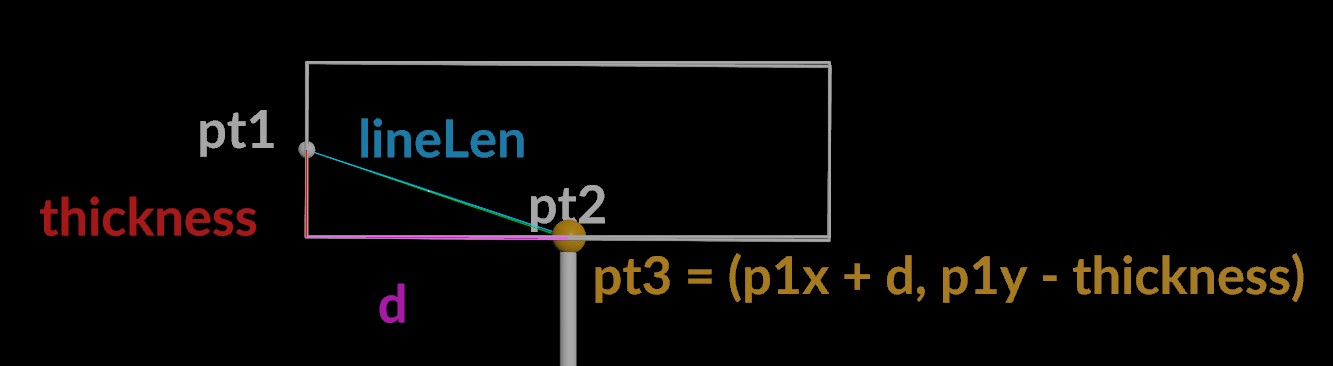
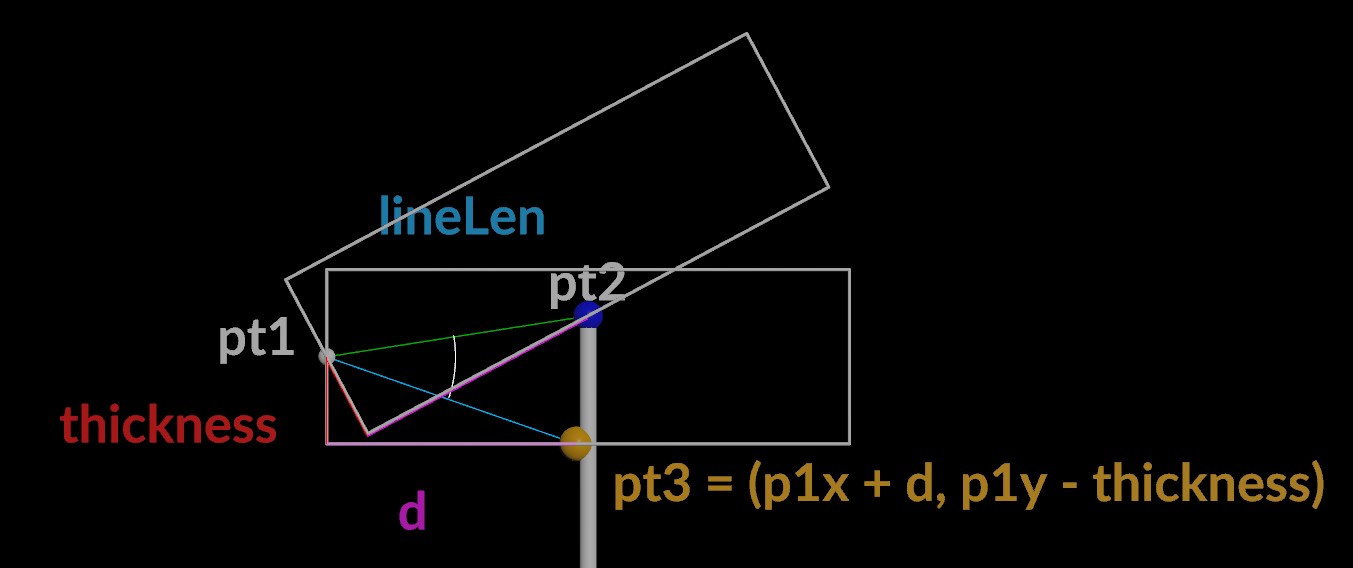
Given the following diagram
We have vector p2 - p1 and we have a vector p3
- p1 where p3 is d over in x and -thickness over in y given the
box.
So the angle between the two vectors is the amount we need to
rotate so that p3 is in position p2
@dotresult =
degrees(acos(dot(normalize(v@pt2-v@pt1),normalize(v@pt3-v@pt1))));

Note that @d is calculated by taking the sqrt of lineLen squared - thickness squared thanks to Pythagorean's theorem.
In a right angle triangle, hyp squared = side1 squared + side2 squared therefore we subtract thickness and take the sqrt.
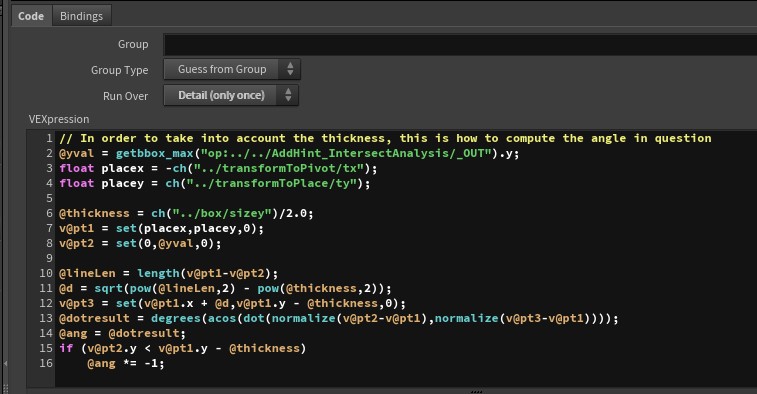
This is the correct solution. It is worth nothing that a quick cheat with atan gets pretty close, but not completely accurate.
The results of simply taking the thickness away from the calculation in y comes very close. The "cheat" using the hscript expression result is show in yellow. The correct one is shown in white.
Inaccurate cheat:
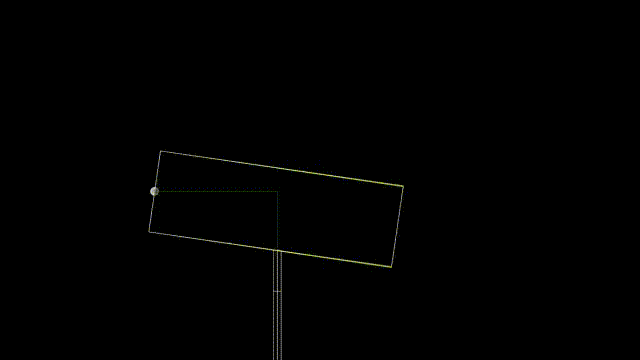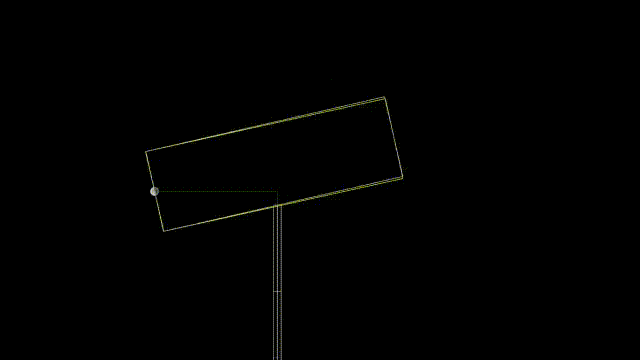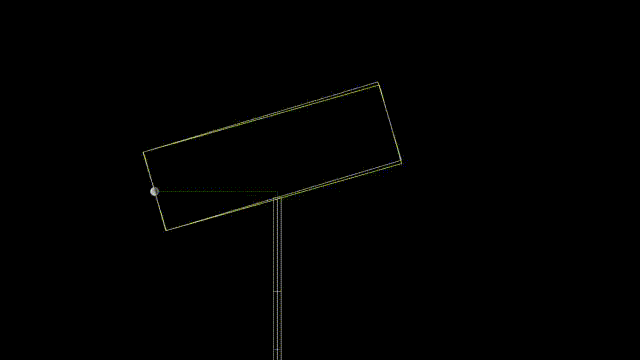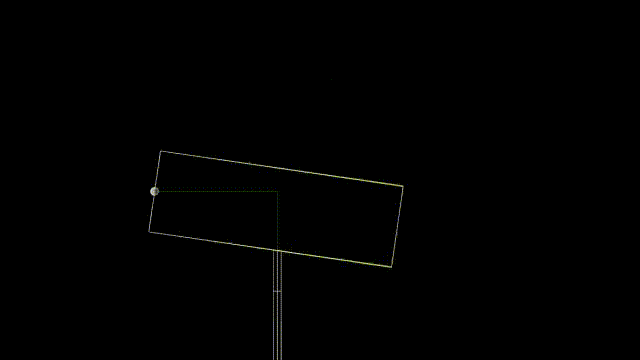
Note that we could also be more accurate by using two lines to approximate the tube rather than just one. I have done so in my arbitrary gear rotation example https://www.youtube.com/shorts/WOwYyI11xSk or
https://vimeo.com/687726753