Deborah R. Fowler
Tire Rotation
Posted on Nov 25 2017
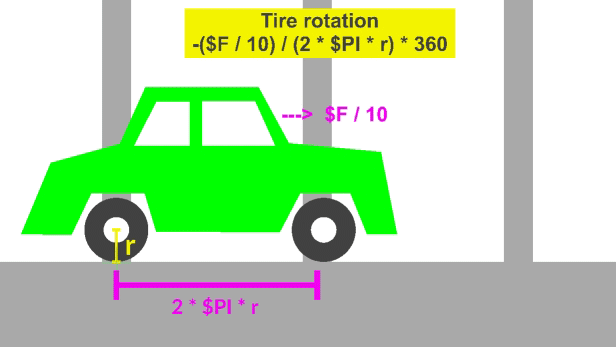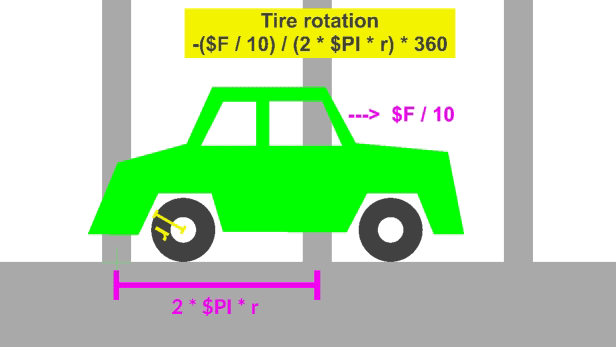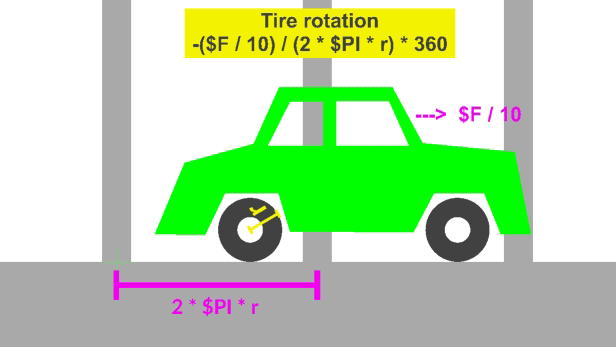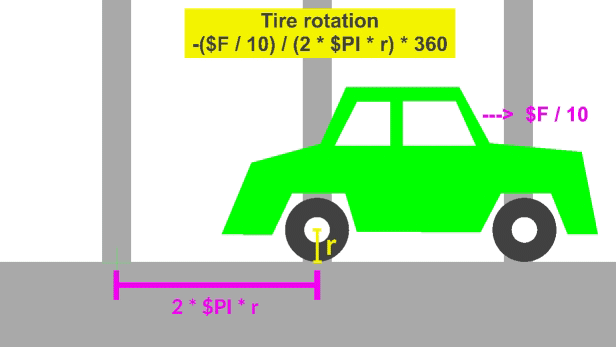
Recall that the circumference of a circle is 2 * PI * radius

A tire on a car will travel 2 * PI * r units / revolution. The pillars in the video below were place this distance apart.
Watch the back tire and you will see it aligns with the pillars.

This is true for any radius.
Or any speed. So how does speed of the vehicle factor in? The two figures above are moving at $F/10. The one below is moving at $F.

If a vehicle is traveling at say 10 units / sec if you need to know the revolutions (rev) / sec for the tire
Take 10 units / sec and divide by 2 * PI * r units / rev
This gives you 10 units / sec * 1 / ( 2 * PI * r ) rev / units
Thus 10
So now you have an equation to calculate rev per sec
However, our rotation values are in degrees and there are 360 degrees / rev
So to get the tire speed we multiply rev / sec * degrees / rev to give us degrees / sec
Since we are using $F for both, this is what it looks like in Houdini:
The distance traveled by the car is tx = ($F / 10) and in that distance the tire needs to rotate the following amount:
(car tx at a given time step) / (2 * PI * r) * 360
I find it helpful to think of the fractions ( units / time step ) / ( units / rev ) * ( degrees / rev )
which re-written is