Deborah R. Fowler
Wrangle Node
Example - Tangent to Circle
Posted on May 21 2018
Update on Nov 10 2020 added example in z and y axis as
well
Example file starter here: hipnc available
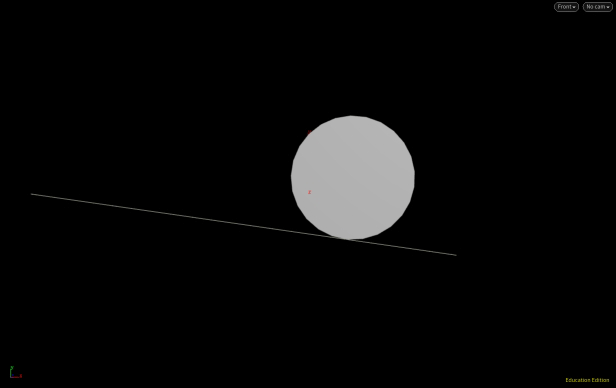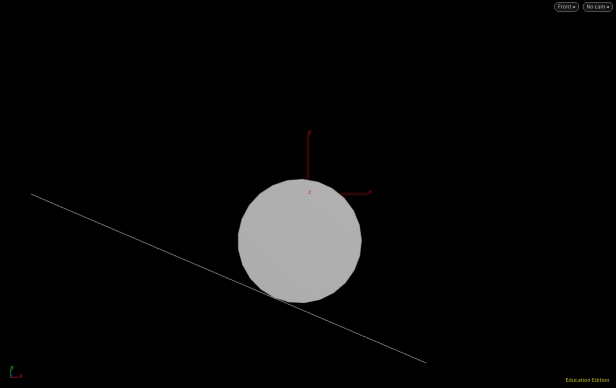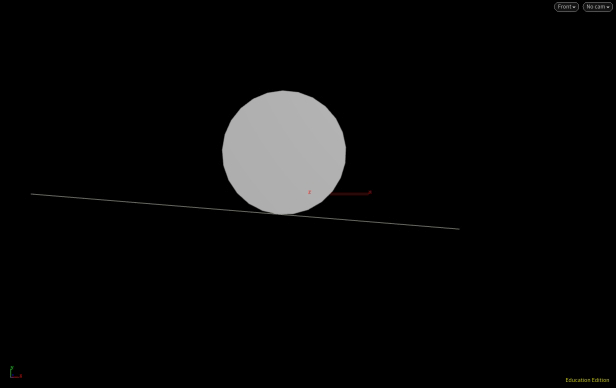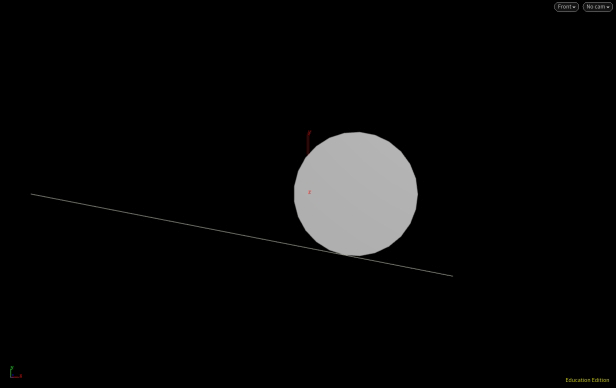
The goal was to find a tangent to the circle. Keep in mind this has been set up for a specific problem and may need to be modified for particular use since there are two solutions to a tangent to a circle.
The solution can be found by defining the triangle relationships at any given point in time and taking the arc sine (opposite over hypotenuse).
The pivot point of the green rod in question is rotated relative to the x-axis. However, if you look at the angle between the purple and green lines, we can calculate the purple line, below we label it D.
D is a vector determined by its two endpoints, pt0 and pt1 - these are plugged into the point wrangle. I have set them to attribute for viewing in the geometry spreadsheet (not necessary, could use local variables).
Since we know D, and we know that r (radius of the circle) and the tangent is perpendicular to the circle by definition, we have the opposite and the hypotenuse of a right angle triangle.
Thus we take the asin(r/D). However, this only gives us the angle between the purple and green rods. Rotation is defined from the x-axis.
Happily, we can find that angle (between the red and purple vectors) by noting that the value is y1 from the horizontal, and D is the hypotenuse, so again we have asin(y1/D).
The result here is negated since we are going in the opposite direction that angles usually go (ie. clockwise, whereas if we were solving for the other tangent of the circle we would go counter clockwise)
Below I have written asin(@r/@D) - asin(Pt1.y/@D) which is really the same as asin(@r/@D) + asin(-Pt1.y/@D)
A diagram shows that this is being calculated correctly even though the circle's center is changing (we have used an add node with $CEX, $CEY, $CEZ).
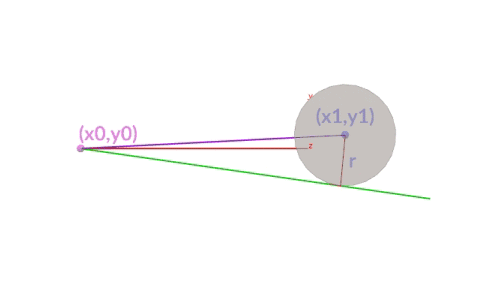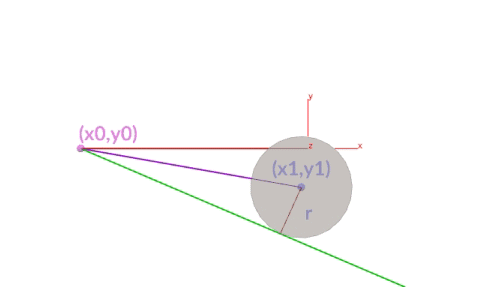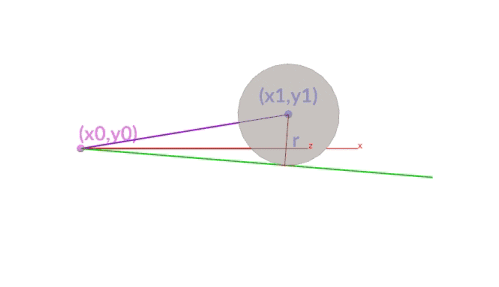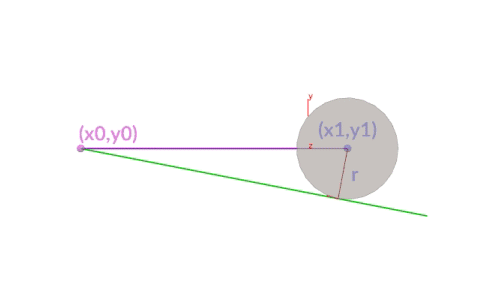
In a similar case, May 15 2019 the equation changes slightly as the position and orientation of the rod differs

Point wrangle is as follows:
With the node network and two points coming into the point wrangle shown above. Note: to retrieve a details attribute use detail("../pointwrangle1","rotAngle",0)
In a similar case, Nov 10 2020, where a z-axis and y-axis are used. Same theory, slight tweaks to the pointwrangle node. I have also added some geometry to show how easy it is to convert the lines to geo with a sweep node.
created in Houdini 18.0.499 tangentTpCircleOtherAxis.hipnc
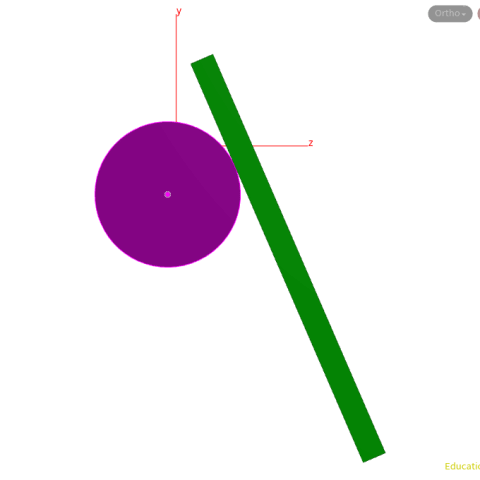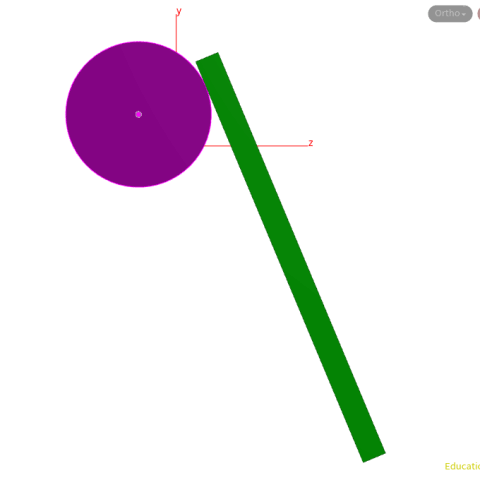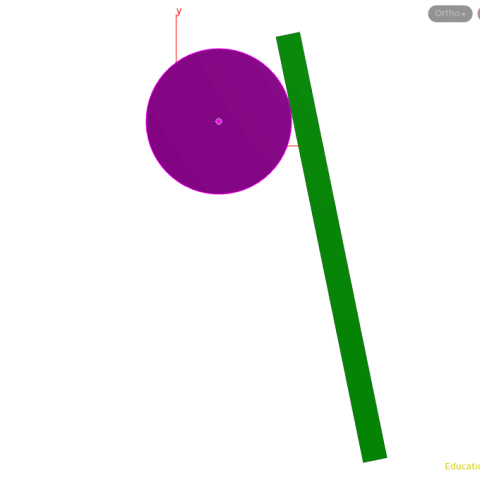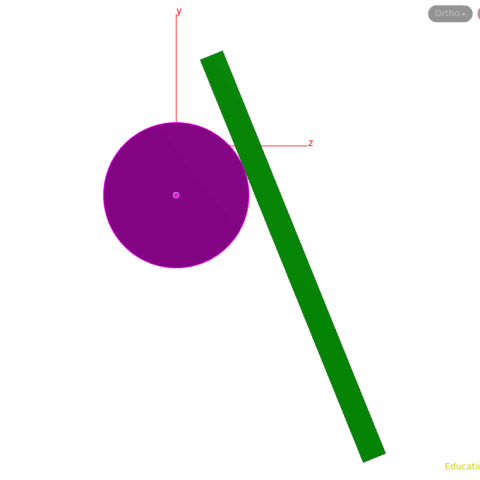
This could be used to create an interesting animation.