Deborah R. Fowler
Dot Product - Any polygon
Posted Nov 25 2020
updated on Dec 8 2020 adding video links
updated on June 19 2020 adding links to further
generalizations
Tags: point wrangle, attribute
promote, dot product, acos, normalize, length
"Dot Product is the product of the magnitudes of the two vectors and the cosine of the angle between them. The name "dot product" is derived from the centered dot "
"
that is often used to designate this operation." See wiki entry.Also on youtube at https://www.youtube.com/watch?v=UqpmteoWF6s
MECHANICS
This project was inspired by two things:
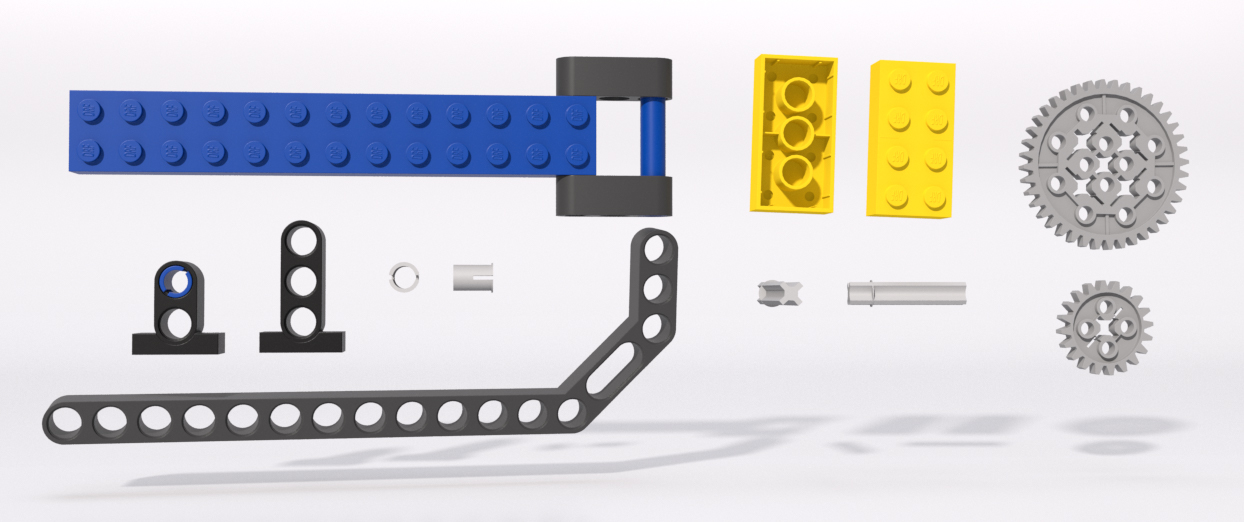
- a piece of a toy that my son had in a toy bin of lego (when I wanted an object with a hinge)
- when teaching students about bbox
,
intersection analysis 
for
automaton (see
tips and tricks), and tangent
to a circle 
(wrangle
node examples) these all work fine, except in the case of an
arbitrary polygon moving a lever. Most of the examples to date
have not required a solution to this problem but I was just
thinking about the tangent to a circle and what if it was not
a circle ...
It started off with a simple geometric proof of concept and one line of pointwrangle code:
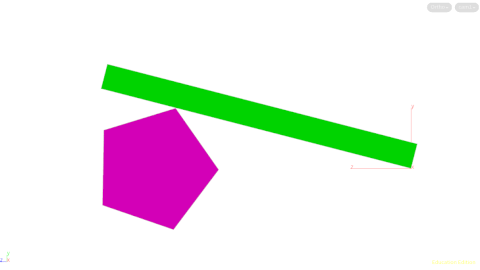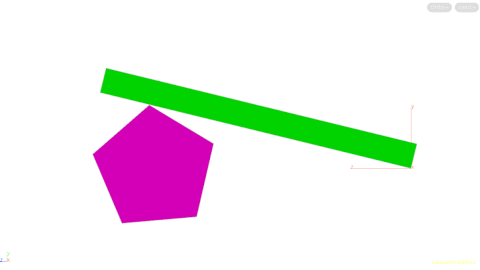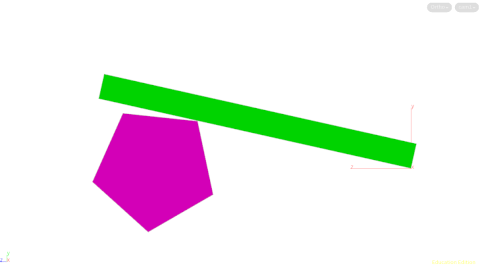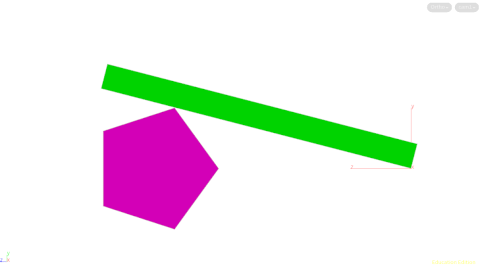
The key to the solution is to calculate the dot product between the axis (z-axis in this case) and each point of the polygon. Then take the acos to find out the angle and convert it into degrees for use in the hscript expression. I love math!
The point that needs to be used is the maximum angle. A really useful method for doing this in Houdini is to use Attribute Promote and promote the parameter to detail and select the maximum value. Sweet! I love Houdini!
- I also used a clip node to reduce computation (less points)
- I wanted this to work on an arbitrary 3D shaped polygon. In
this case it is imperative to scale to
0 in x so that you are only dealing with the
distance from the point P to the origin in one dimension,
otherwise some points are giving a larger value but not accurate
for pushing up the lever (longer in three dimensions).
That seemed like an excellent solution to the problem. Done. But ...
After deciding on a model to use (see modeling section below for details) the next step was to figure out how the problem applied if instead of rotating the line corresponding to a line at the bottom part of a box we were rotating around the origin with the box shown below. This is where it becomes similar to the tangent to a circle problem, but again we are going to do this for every point on the polygon.
MECHANICS - line with "thickness"
The above was based on a line and the box is rotating at the bottom point, however most often we want the line to have "thickness". The example below has the box centered as the model I will use.
Now the problem is not just the line crossed with the z-axis as above. We need to focus on the green box rotation. The solution is as given in the point wrangle, with the explanation below
We can generalize this even further by adding the ability to go up and down. See the "Spin" example by cliicking here.
MODELING
I started to think about what kind of example I could create that was not just a line and also tried objects that were 3D. This is where it gets a bit more interesting (and similar to the tangent to the circle).
My inspiration (yes, reference, reference, reference) was from a pieces of lego from my son's toy bin, and some gears I found pictures of online.
